class 8 : maths :Parallel lines and transversals : Practice set 2.1
QUE 1. In the adjoining figure, each angle is shown by a letter. Fill in the boxes with the
help of the figure.
Corresponding angles.
i. ∠p and __
ii. ∠q and __
iii. ∠r and __
iv. ∠s and __
Interior alternate angles:
v. ∠s and __
vi. ∠w and __
ANSWER :
i. ∠w
ii. ∠x
iii. ∠y
iv. ∠z
v. ∠x
vi. ∠r
QUE 2. Observe the angles shown in the figure and write the following pair of angles
(1) Interior alternate angles
(2) Corresponding angles
(3) Interior angles
ANSWER :
- ∠c and ∠e; ∠b and ∠h
- ∠a and ∠e; ∠b and ∠f; ∠c and ∠g; ∠d and ∠h
- ∠c and ∠h; ∠b and ∠e
class 8 : maths :Parallel lines and transversals : Practice set 2.2
1. Choose the correct alternative.
(1) In the adjoining figure, if line m || line n and line p is a transversal then find x.
(A) 135° (B) 90° (C) 45° (D) 40°
(C) 45°
ANSWER :
line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x =
∴ x = 45°
(D) 30°
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x =
∴ x = 30°
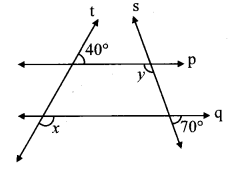
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°
Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°
ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]
iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°
4. In the adjoining figure, line a || line b. line l is a transversal. Find the measures of ∠x, ∠ y, ∠z using the given information
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]
ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]
iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°
5. In the adjoining figure, line p || line l || line q. Find ∠ x with the help of the measures given in the figure.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°
class 8 : maths :Parallel lines and transversals :Practice set 2.3
1. Draw a line l. Take a point A outside the line. Through point A draw a line parallel to line l
ANSWER :
(1) Draw a line l. Take a point A outside the line l.
(2) Draw a segment AM ⊥ line l.
(3) Take another point N on line l.
(4) Draw a segment NB ⊥ line l, such that l(NB) = l(MA).
(5) Draw a line m passing through the points A and B.
Hence, the line m is the required line that passes through point A and parallel to line l.
2. Draw a line l. Take a point T outside the line. Through point T draw a line parallel to line l
ANSWER :
Steps of construction :
(1) Draw a line l. Take a point T outside the line l.
(2) Draw a segment MT ⊥ line l.
(3) Take another point N on line l.
(4) Draw a segment NV ⊥ line l, such that l(NV) = l(MT).
(5) Draw a line m passing through the points T and V.
Hence, the line m is the required line that passes through point T and parallel to line l.
3. Draw a line m. Draw a line n which is parallel to line m at a distance of 4 cm from it
Steps of construction :
(1) Draw a line m.
(2) Take two points A and B on the line m.
(3) Draw perpendiculars to the line m at A and B.
(4) On the perpendicular lines, take points P and Q at a distance of 4 cm from A and B respectively.
(5) Draw a line n passing through the points P and Q.
So, line n is the required line parallel to the line m at a distance of 4 cm away from it.