Class 8 : maths : Rational and Irrational numbers : Practice set 1.1
QUE : (1). Show the following numbers on a number line. Draw a separate number line
for each example.
i.
ii.
iii.
iv.
ANSWER :
(i.) 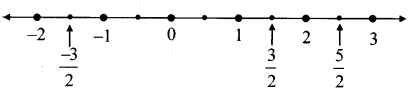
Here, the denominator of each fraction is 2.
∴ Divide each unit into 2 equal parts.
ii. 
Here, the denominator of each fraction is 5.
∴ Divide each unit into 5 equal parts.
iii. 
Here, the denominator of each fraction is 8.
∴ Divide each unit into 8 equal parts.
iv. 
Here, the denominator of each fraction is 10.
∴ Divide each unit into 10 equal parts.
QUE : 2. Observe the number line and answer the questions.
Observe the number line and answer the questions.
i. Which number is indicated by point B?
ii. Which point indicates the number
iii. State whether the statement, ‘the point D denotes the number
Solution:
Here, each emit is divided into 4 equal parts.
i. Point B is marked on the 10th equal part on the left side of O.
∴ The number indicated by point B is
ii.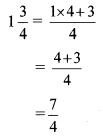
Point C is marked on the 7th equal part on the right side of O.
∴ The number
iii. True
Point D is marked on the 10th equal part on the right side of O.
∴ D denotes the number
Class 8 : maths : Rational and Irrational numbers : Practice set 1.2
QUE : 1. Compare the following numbers.
i. 7, -2
ii. 0,
iii.
iv.
v.
vi.
vii.
viii.
ix.
x.
Solution:
1]. 7, -2
If a and b are positive numbers such that a < b, then -a > -b.
Since, 2 < 7 ∴ -2 > -7
2]. 0,
On a number line,
∴ 0 >
3] .
On a number line, zero is to the left of
∴
4].
We know that, a negative number is always less than a positive number.
∴
5].
Here, the denominators of the given numbers are the same.
Since, 40 < 141
∴
6].
Here, the denominators of the given numbers are the same.
Since, 17 < 13
∴ -17 < -13
∴
7].
Here, the denominators of the given numbers are not the same.
LCM of 12 and 16 = 48
8].
Here, the denominators of the given numbers are not the same.
LCM of 8 and 4 = 8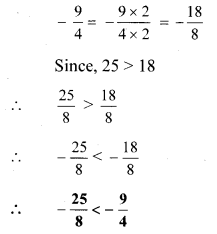
9].
Here, the denominators of the given numbers are not the same.
LCM of 15 and 5 = 15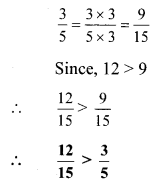
10].
Here, the denominators of the given numbers are not the same.
LCM of 11 and 4 = 44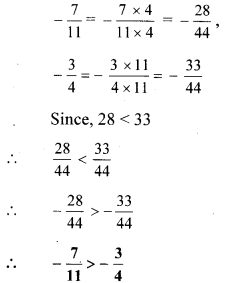
Class 8 : maths : Rational and Irrational numbers : Practice set 1.3
QUE :1. Write the following rational numbers in decimal form.
1].
2].
3].
4].
5].
ANSWER :
1]. 
2]. 
3]. 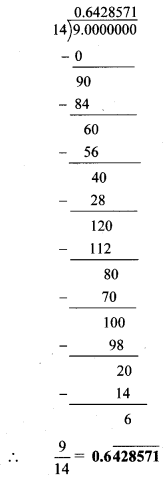
4]. 
5]. 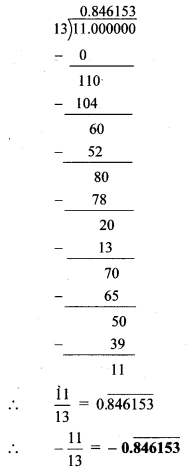
Class 8 : maths : Rational and Irrational numbers : Practice set 1.4
QUE :1]. The number √2 is shown on a number line. Steps are given to show 3 on the number line using √2. Fill in the boxes properly and complete the activity.
The point Q on the number line shows the number ……….
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3
Solution:
The point Q on the number line shows the number √2
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
.. .[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.
QUE : 2] Show the number 5 on the number line.
ANSWER :
Draw a number line and take a point Q at 2
such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴l(OR) = √5 units
…[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the number line and arc as C. The point C shows the number √5.
QUE :3]. Show the number 7 on the number line.
ANSWER :
Draw a number line and take a point Q at 2 such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴ l(OR) = √5 units
… [Taking square root of both sides]
Draw an arc with centre O and radius OR.
Mark the point of intersection of the number line and arc as C. The point C shows the number √5.
Similarly, draw a line CD perpendicular to the number line through the point C such that l(CD) = 1 unit.
By Pythagoras theorem,
l(OD) = √6 units
The point E shows the number √6 .
Similarly, draw a line EP perpendicular to the number line through the point E such that l(EP) = 1 unit.
By Pythagoras theorem,
l(OP) = √7 units
The point F shows the number √7.





